韩信点兵 历史故事（韩信点兵的故事简写）

三齐王指韩信。韩信平定齐地后，被封为齐王。“三齐”是指项羽在战国的齐国故地上分封的三个国家。“三齐王”大概是指韩信是战国时期的齐国故地的实际统治者。

相传三齐王韩信才智过人，从不直接清点自己军队的人数，只是让士兵先后以三人一排、五人一排、七人一排地变换队形，而他每次只掠一眼队伍的排尾就知道总人数了（不超过100人）。

物不知数

韩信点兵问题最早出自《孙子算经》。《孙子算经》是中国古代非常重要的数学著作，因数学家 孙子 贡献最大而得名（关于孙子的资料不可考），大约成书于东晋十六国时期，现存最早为北宋刻本，全书分三卷：《卷上》、《卷中》、《卷下》，主要讲述 度量规定 和 算筹运算 以及基于 它们的 数学应为问题，韩信点兵为 《卷下》第二十六题 ”物不知数“，原文如下：

今有物，不知其数。三、三数之，剩二；五、五数之，剩三；七、七数之，剩二。问物几何？

答曰：二十三。

术曰：“三、三数之，剩二”，置一百四十；“五、五数之，剩三”，置六十三；“七、七数之，剩二”，置三十。并之，得二百三十三。以二百一十减之，即得。凡三、三数之，剩一，则置七十；五，五数之，剩一，则置二十一；七、七数之，剩一，则置十五。一百六以上，以一百五减之，即得。

题目翻译成现今的数学语言如下：

有一个正整数 x，知 x 除以 3 余 2、除以 5 余数 3、除以 7 余数 2， 求 x 的最小值。

这等价于求解《初等数论》中的 一次同余方程组：

《孙子算经》给出的解法如下：

寻中最小正整数 x? ， 满足： x? 被 5 和 7 整除 并且 除以 3 余 1，即，5|x?, 7|x? 并且 x? mod 3 = 1 ②

x? 被 5 和 7 整除，就意味着 被 5×7 = 35 整除，即， 35 | x?，于是，令 x? = 35n（n ≥ 1）：

当 n = 1 时 x? = 35，35 mod 3 = 2 不满足 ② 舍弃；

当 n = 2 时 x? = 70，70 mod 3 = 1 刚好满足 ②，Bingo~~~。

由于 x? ≡ 1 (mod 3)，故 2x? ≡ 2 (mod 3)，于是 得到 2x? = 140，它满足：除以 3 余 2 并且 被 5 和 7 整除。

同理，

求得满足：可被 3 和 7 整除 并且 除以 5 余 1 的最小正整数 x? = 21，从而得到，同样可被 3 和 7 整除 但 除以 5 余 3 的 3x? = 63；

求得满足：可被 3 和 5 整除 并且 除以 7 余 1 的最小正整数 x? = 15，从而得到，同样可被 3 和 5 整除 但 除以 7 余 2 的 2x? = 30；

将上面的 结果 相加 得到： x’ = 2x? + 3x? + 2x? = 140 + 63 + 30 = 233，则 容易验证 x‘ 是 同余方程组 (1) 的一个解 ，但是 x’ 不是 最小整数解 x。很容易可以发现 x' 减去 一个 同时 被 3、5 和 7 整除 并且 不大于 x' 的 整数，结果依然 是 (1) 的解，由于，同时 3、5 和 7 整除，就 意味着 被 3×5×7 = 105 整除，于是得出：

x = x' (mod 105)

进而，有如下算法：

令 x = x'；

如果 x > 105（原文为 106 = x? + x? + x? ） 则 令 x = x - 105，否则 x 为 最终答案；

具体过程如下：

x = x' = 233

[x = 233 > 105]： x = x - 105 = 233 - 105 = 128

[x = 128 > 105]： x = x - 105 = 128 - 105 = 23

[ x = 23 < 105]：OK！

这样就得到了最终答案：x = 23。

将整个求解过程写成算式就是：

x = 2×70 + 3×21 + 2×15 - 2×(3×5×7) = 23

为了方便记忆，发明 珠算 和 卷尺 的明朝数学家 程大位，在其所著的 《算法统宗》 中，将 《孙子算经》的算法编成 "孙子歌诀" 如下：

三人同行七十稀，

五树梅花廿一枝，

七子团圆正半月，

除百零五便得知。

注：正半月就是十五天，除是除去（减去）之意。

韩信点兵

韩信点兵 泛指 ”物不知数“ 此类 一次同余方程组 求解问题。南宋著名数学家 秦九韶 对 《孙子算经》中的算法 进行了深入研究，将其扩展为『大衍总数术』，彻底解决了 韩信点兵问题，这就是 《初等数论》中的 中国剩余定理（也称 孙子定理）：

设 m?, m?, ..., m_n 是 两两互素 的 正整数，那么对于任意整数 a?, a?, ..., a_n 组成的 一次同余方程组：

在同余意义下，必有唯一解：

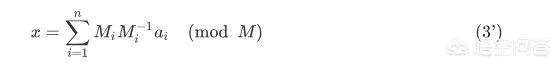
其中：

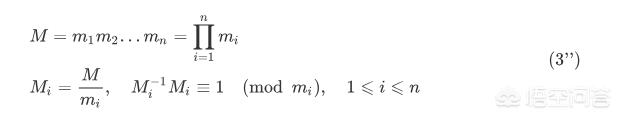
验证：易知，

再结合 (3'')，由 (3') 可以推出：

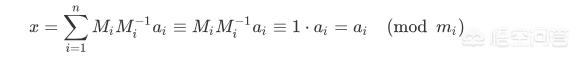
这就说明 (3') 的确 是 (3) 的解。

注：这里只是给出了定理的验证，并没有严格证明 同余意义下的唯一性。证明 中国剩余定理，有多种方法大家有兴趣可以参考《初等数论》。

秦九韶 分别称 M、M? 、 M??1 为 衍母、衍数、乘率，这里的关键是求 乘率 M??1 ，方法如下：

令， r 是 M? 除以 m? 的余数，即，

于是：

进而：

然后，让 m? 和 r 辗转相除，得到：

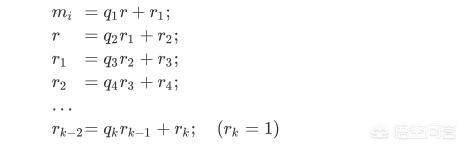
到 r_k = 1 终止。如果 向下进行一步就是：

前面再加上 (4) ，整个过程 就是 欧几里得辗转相除法，因此 r_k 为 M? 和 m? 的 最大公约数，而 m?, m?, ..., m_n 是 两两互素，于是有： r_k = (M?, m?) = 1 ，这样就证明了 最后 总可以 终止于 1 的正确性。

接着，定义两个数列：

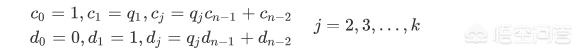
有：

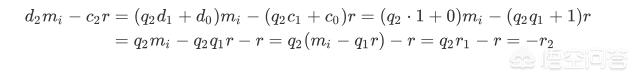
即，

假设，

则：

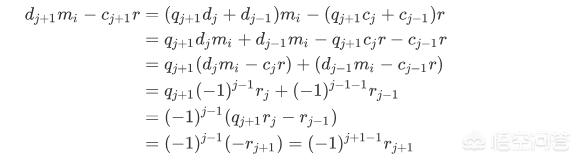
这样归纳的证明了 (7) 成立。

当 k 为偶数时 有：

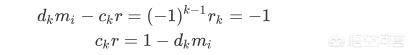
于是：

比较 (5) 得到：

当 k 为奇数时，则 k + 1 是偶数，这就要算到 (6) ，对 (6) 稍作变形：

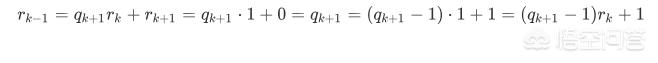于是，令，

并重新令：

则有：

这样我们就将 辗转相除 又延长了一步 到 k + 1，这时 k + 1 是偶数，则同理上面 情况 可得到：

因为此算法最后总会终止于 1，所以 被 秦九韶 称为『大衍求一术』，前缀 “大衍” 来自于《易经 · 系辞》：“大衍之数五十，... ...”。

当然，中国剩余定理 要求 m?, m?, ..., m_n 必须两两 互素，对于那些 不满足这个条件的 一次同余方程组 可以转换为 和 其 同解 的 满足这个条件的 一次同余方程组。下面举例说明：

有一筐鸭蛋，1个1个数，正好数完；2个2个数，还剩1个；3个3个数，正好数完；4个4个数，还剩1个；5个5个数，还剩1个；6个6个数，还剩3个；7个7个数，正好数完；8个8个数，还剩1个；9个9个数，正好数完。请问：框里最少有多少个鸭蛋？

按照题目所述，列同余方程组如下：

显然 1, 2, 3, 4, 5, 6, 7, 8, 9 并不两两互素，因此需要简化：

一个数字必然被 1 整除，因此 ① 没有意义，删除； 一个数字被 9 整除，必然会被 3 整除，因此 保留 ⑨ 删除 ③；一个数字 被 8 除余 1，则可以表示为 8x + 1，进而有 2(4x) + 1，4(2x) + 1，于是 x 一定 可以被 2 和 4 整除，因此 保留 ⑧ 删除 ② 和 ④；目前已经保证了 被 2 除 余 1，可表示为 2x + 1，也保持了 被 3 整除，于是有 3(2x + 1) = 6x + 1，这说明 目前已经保持了 被 6 除 余 3，因此 ⑥ 可以被删除；最后剩下 ⑤ 和 ⑦ 保留。得到：

则 (8') 和 (8) 等价。由于 5,7,9,8 两两互素，符合 中国剩余定理 要求，于是解：

◆M = m? m? m? m? = 5 × 7 × 8 × 9 = 2520

◆M? = 7 × 8 × 9 = 504

M? = q m? + r, 504 = 100 × 5 + 4 , c? = 1;

m? = q? r + r?, 5 = 1 × 4 + 1, c? = q? = 1; (r? = 1，下标 1 是奇数，需要再算一步 )

r = q? r? + r?, 4 = 3 × 1 + 1, c? = q?c? + c? = 3 × 1 + 1 = 4；(得到结果)

M??1 = 4， M??1 M?a? = 4 × 504 × 1 = 2016；

◆ 由于 a? = 0 所以 M??1 M?a? = 0；

◆M? =5 × 7 × 9 = 315

M? = q m? + r, 315 = 39 × 8 + 3 , c? = 1;

m? = q? r + r?, 8 = 2 × 3 + 2, c? = q? = 2;

r = q? r? + r?, 3 = 1 × 2 + 1, c? = q?c? + c? = 1 × 2 + 1 = 3；(r? = 1，下标 2 是偶数，得到结果)

M??1 = 3， M??1 M?a? = 3 × 315 × 1 = 945；

◆由于 a? = 0 所以 M??1 M?a? = 0；

得到：

x = M??1 M?a? + M??1 M?a? + M??1 M?a? = 2016 + 0 + 945 + 0 = 2961

x > M, x = x - M = 2961 - 2520 = 441

最终答案：框里最少有 441 个鸭蛋。

最后，需要说明的是：

数学大神欧拉和高斯 对于 一般一次同余式进行了详细研究，独立的得到了 中国剩余定理，后来证实 与 秦九韶『大衍求一术』相同，于是才命名该定理为：中国剩余定理。

中国剩余定理，在《抽象代数》中还有另外的形式，不过这就扯远了，就此打住。

（由于本人数学水平有限，出错在所难免，欢迎各位老师批评指正！）

展开全部

你好。

【韩信暗点兵】歌诀：

三人同行七十夕，五数梅花二十一，七子团圆正半月，去百零五便得知。

韩信暗点兵，韩信不是一、二、三、点数，而是，让队伍列队：

首先三人一列，记住多余的人数；

再让五人一列，记住多余的人数；

再做七人一列，记住多余的人数。

将上面三次多余的人数相加。他就知道一共有多少人。

计算：

三列队的余数，比如说，余数是二。则：2*70=140 （余数不可能多余二）

五队列的余数，比如说，余数是四，则：4*21=84 （余数不可能多余四）

七队列的余数，比如说，余数是六，则：6*15=90 （余数不可能多余六）

上列结果相加：140+84+90=314

假如说，一估计，没有300多人，就：314—105=209

假如一看，还没有200多人，再减去105，则：209——105=104

好。就是104人。

注：这里面除了上面的计算以外，还要估算一下。大约数再进行比较计算。